Fret Calculations for Just Intonation and its Effect on Modes
As we all know, traditionally the dulcimer was a drone instrument where a fretted melody string was played against drones. And traditionally the root note of the diatonic scale was placed at the 3 rd fret (a perfect 4 th above the open melody string and/or octave above the bass drone). A dulcimer's staple frets would have been set by ear. Although a maker 'could' set the frets by ear with just one string on the instrument (if they had perfect pitch!) it is far easier to set the frets by ear when using two strings one as a sonic reference and one under which the fret wire is placed. The fret wire can then be moved around until the desired note blends perfectly with the drone string, the position marked, and the fret then placed.
This system for setting the frets leads to just intonation as it is far easier to find harmony than it is to find the dissonance of a tempered scale system. When we sing a cappella, particularly when singing in harmony, we naturally slip into just intonation. So if you are playing dulcimer with drones then just intonation produces the natural harmonies our ears like.
Having played a number of older dulcimers by the likes of the Glens, Presnell, Ledford, Tignor, Jeffries etc they all show the traits of just intonation with flattened 3rds, 6ths and 7ths and perfect 4ths and 5ths. There is no doubt that some of these makers would have perhaps set-up an early build by ear and then drawn a template of the fret layout and used that for future instruments (sometimes building in compound errors!).
However, there is a mathematical way to calculate the fret positions for just intonation that's been around for almost 2000 years and was first put to pen by Ptolemy (AD 90-168). Ptolemy produced the calculations for his 'intense diatonic scale', which is based on the harmonic vibrations of a mono-chord (a single string instrument). If you take a string and stop it at the mid point you get an octave if you stop it at a third of its length you get a perfect 5 th if you stop it at a quarter of its length you get a perfect 4 th etc etc. So you end up with simple fractions that determine the harmonic frequencies of pitch that blend with the root note in harmony. These fractions are shown in this table taken from Wikki:
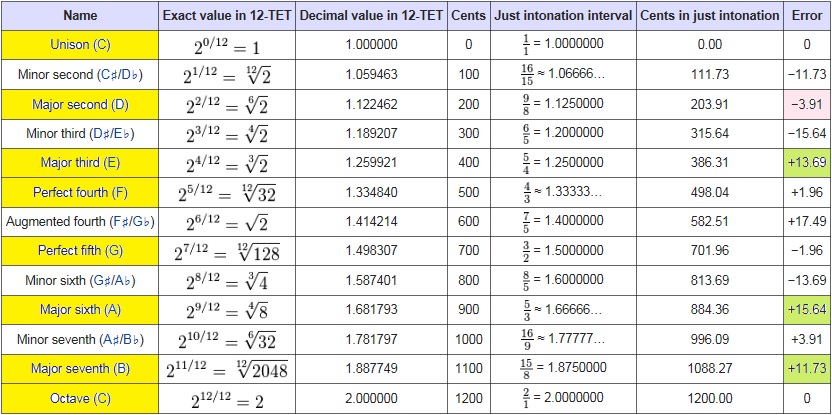
You can see from this table the differences between equal temperament fretting and just intonation in particular the 3rds, 6ths and 7ths are slightly flatter and the 4ths and 5ths are perfect. In equal temperament every fret is just a little out of tune and that's why it is known as a 'tempered' scale. Quarter comma mean tone is also a tempered scale but it is centred on achieving a perfect 3 rd and then adjusting the spaces between the notes from that point. It is closer to just intonation than equal temperament and also allows some leeway in shifting keys without re-tuning. In just intonation you will have to re-tune to shift keys but seeing as that is how noter drone dulcimer is played it is not an issue for us.
The intervals for just intonation are simple fractions based on the harmonic vibration of the string: 1/1 unison, 9/8 major second, 5/4 major third, 4/3 perfect fourth, 3/2 perfect 5th, 5/3 major sixth, 15/8 major seventh, 2/1 octave. Make a note of these ratios as you will be continuously coming back to them as you calculate your fret positions. Today I measures my Clifford Glen dulcimer and it is fretted very, very close to these ratios.
To turn these simple fractions into fret placements requires a little thought and some mathematics!
Let's start with your actual VSL and takea 28.5 scale as an example. It is easier to work in millimetres as we will be dealing with decimal places. The physical scale for 28.5" is say 725 mm but the fret spacing is actually calculated from a hypothetical VSL of 722 mm as this allows3 mm for better intonation of the higher frets caused by the higher action closer to the bridge. Many dulcimer makers will calculate their fret placements using a fractionally shorter VSL than the actual measurement from nut to bridge.
Our first job is to find the position of the 3 rd fret the root note of our diatonic scale. In 1-5-5 tuning this note will be a perfect 4 th above the open string and a perfect octave above the bass string. Mathematically these two positions harmonise perfectly when the bass string and melody strings are set a perfect 5 th apart. In equal temperament this is not the case!!!! Have you ever wondered why when you tune your dulcimer to DAA the 'd' root note at the 3 rd fret is a little sharp? Well that's because in equal temperament the 3 rd fret is set sharp it is not perfectly in tune but in a position of compromise (and so on up the equal temperament scale).
The math to find our 3 rd fret position is pretty straightforward.
VSL of 722 mm divided by 4/3 to get the perfect fourth = 541.50 mm which is the length of the string required to sound a perfect fourth higher. We need to find how far the fret should be from the nut rather than the bridge so we must take 541.5 from 722 = 180.50 mm
So our 3 rd fret will be 180.50 mm from the nut.
We are now going to work out the just intonation scale of do, ra, me, fa, so, la, te, do from the 3 rd fret to the 10 th fret. To do this we need to use a new VSL of 541.50 mm, which is the length from the 3 rd fret to the bridge.
The 4 th fret is the major second of the scale so the calculation is:
VSL of 541.50 divided by 9/8 to get the major second = 481.33 which is the length of string required to sound the major second. Take 481.33 away from our scale length of 541.50 = 60.16 mm, which is the distande between the 3 rd and 4 th frets. Add 180.50 to give us the distance from the 4 th fret to the nut = 240.66 mm
So our 4 th fret is 240.66 mm from the nut.
We can continue using the VSL of 541.50 mm up to the octave at the 10 th fret, remembering to add the 180.50 mm from the nut to the 3 rd fret each time. For the 10 th to the 17 th frets we do a similar process using the VSL of 270.75 which is half of 541.50. Our starting point for the second octave is the 10 th fret which is 451.25 away from the nut so we need to add this amount to each calculation.
Finally we need to find the positions of the first and second frets. If you think about it these two notes are actually the major 6 th and major 7 th of a scale twice the length of the one starting at the third fret. So they need to be calculated from a VSL of 1083 mm. Taking the first fret as an example: The VSL is 1083 mm divided by 5/3 to give the major sixth = 649.80 mm which is the distance from the bridge to the 1 st fret. We need to take 649.80 from 1083 to give 433.20 which is the distance from the hypothetical start point of our 1083 mm VSL to the first fret. However, the nut is actually the 5 th of the 1083 mm VSL so we need to take away 361.00 mm (the distance from our hypothetical nut of the 1083 VSL to the perfect 5 th our real nut position) from our major sixth position of 433.20 to give a first fret position of 72.20 mm from the nut.
Here are the calculations for every fret of a 722 VSL dulcimer (in practice the actual VSL will end up being set around 725 to allow forintonation of the higher frets because of the action/pitch/string gauge - ideally a floating bridge will be fitted to allow some intonation adjustment for different actions, string gauges and pitches):
1st fret - 72.20 mm major 6th of 1083 VSL
2nd fret - 144.40 mm major 7th of 1083 VSL
3rd fret - 180.50 mm perfect 4th of 722 mm VSL and root note for the 541.5 VSL
4th fret - 240.66 mm major 2nd of 541.5 VSL
5th fret - 288.80 mm major 3rd of 541.5 VSL
6th fret - 315.87 mm perfect 4th of 541.5 VSL
7th fret - 361.00 mm perfect 5th of 541.5 VSL and octave of 722 mm VSL
8th fret - 397.10 mm major 6th of 541.5 VSL
9th fret - 433.20 mm major 7th of 541.5 VSL
10th fret - 451.25 mm octave of 541.5 VSL
11th fret - 481.33 mm major 2nd of 270.75 VSL
12th fret - 505.40 mm major 3rd of 270.75 VSL
13th fret - 518.93 mm perfect 4th of 270.75 VSL
14th fret - 541.50 mm perfect 5th of 270.75 VSL
15th fret - 559.54 mm major 6th of 270.75 VSL
16th fret - 577.60 mm major 7th of 270.75 VSL
17th fret - 586.62 mm octave of 270.75 VSL
If you use the above calculations I would recommend you use a floating bridge set around 28.5 " as this will enable you to adjust the bridge position for intonation depending on string gauge, action and pitch.
Here is a diagram showing the 4 x VSLs used to calculate just intonation:

The Modes in Just Intonation
This is a whole new topic! Because a 'by ear' fretted dulcimer will naturally fall to just intonation (as seen on many examples of pre-revival dulcimers) it means that the way we 'hear' the modes on an equal temperament dulcimer is significantly different to the way they sound on a dulcimer with just intonation. For example, when we play the mixolidian scale on an equal temperament dulcimer the only note interval than differs from ionian is the 7 th of the scale. However, in just intonation all the note intervals shift slightly. So in ionian on a just intonation dulcimer the second of the scale is 204 cents higher than the root, but in mixolidian the second of the scale is only 182 cents higher than the root and these intervals vary up the scale. This also means that tuning for the modes is not as straightforward as altering the whole intervals of the open strings. Tune the open strings to DAG using a tuner for example and you will not get any of the frets for the dorian scale to sound in tune. There are dissonances within the modes that we don't hear in equal temperament and this gives each mode more of a character. I seem to remember Jean Ritchie talking about the 'character' of the modes in her teaching material and that difference comes out in the unusual dissonance of just intonation. I have to say that mixolidian, in particular, becomes richer and that dorian becomes 'spooky' as Jean described it!!! Aeolian is more managable and I've always though it interesting that Jean used Aeolian for recordings like 'Shady Grove' on the Pete Segar video rather than Dorian even though Dorian is easier to tune (on an equal temperament dulcimer) I now think that this was due to the nature of the more natural scale fretting pattern she had on her dulcimers.
Just intonation has its drawbacks It will not work at all for DAdd chord melody playing and so will limit any dulcimer to being a drone instrument. However, if you are looking to re-create the sweeter more natural sound of early dulcimers and do not want to go through the fretting by-ear process with staples then using Ptolemy's natural intervals will give you a fretting pattern that should blend perfectly with your drones and also match what you would have achieved by ear (excepting the vagaries of very high nuts and bridges!!!).
If you are looking for something not quite so radical then consider a quarter comma mean tone fretting pattern which will still sweeten the 3 rd and 6 th of the scale for you but not place the 4 th and 5 th as 'perfect' (although you don't get them 'perfect' in equal temperament either!!!).

